Yuankai Teng, Quantitative Analytics Specialist at WellsFargo

Yuankai Teng (滕远凯)

slooowtyk at outlook.com

PhD in Applied and Computational Math graduated from the University of South Carolina. My advisors are Prof. Lili Ju and Prof. Zhu Wang. Before that, I did my undergraduate studies at Wuhan University, where I worked with Prof. Xiaoping Zhang.

My PhD research focused on Deep Learning based methods for Scientific Computing. I am now a Quantitative Analytics Specialist at Wells Fargo.

No difference, I care or not.

Publications

Link to [Google Scholar]

A Deep Learning Method for the Dynamics of Classic and Conservative Allen-Cahn Equations Based on Fully-Discrete Operators
Yuwei Geng, Yuankai Teng, Zhu Wang, Lili Ju

Journal of Computational Physics (JCP) [JCP] [code]

The Allen-Cahn equation is a well-known stiff semilinear parabolic partial differential equation (PDE) used to describe the process of phase separation in multi-component physical systems, while the conservative Allen-Cahn equation is a modified version of the classic Allen-Cahn equation that can additionally conserve the mass. Both equations have been popularly used in phase field modeling, and much effort has been devoted to developing conventional numerical methods to compute their solutions. As deep learning has achieved significant successes in recent years in various scientific and engineering applications, there has been growing interest in developing deep learning algorithms for numerical solutions of PDEs. In this paper, we propose and study a deep learning method for simulating the dynamics of the classic and conservative Allen-Cahn equations. We design two types of convolutional neural network models, one for each of the Allen-Cahn equations, to learn the corresponding fully-discrete operators between two adjacent time steps. Specifically, the loss functions of the proposed models are defined as the residuals of the fully-discrete systems of the target equations, which result from applying the central finite difference discretization in space and the backward Euler approximation in time. This approach enables us to train the models without requiring ground-truth data during the training process. Moreover, we introduce a novel training strategy that automatically generates useful samples along the time evolution to facilitate effective training of the models. Finally, we conduct extensive experiments to demonstrate the outstanding performance of our proposed method, including its dynamics prediction and generalization ability under different scenarios in two and three dimensions.

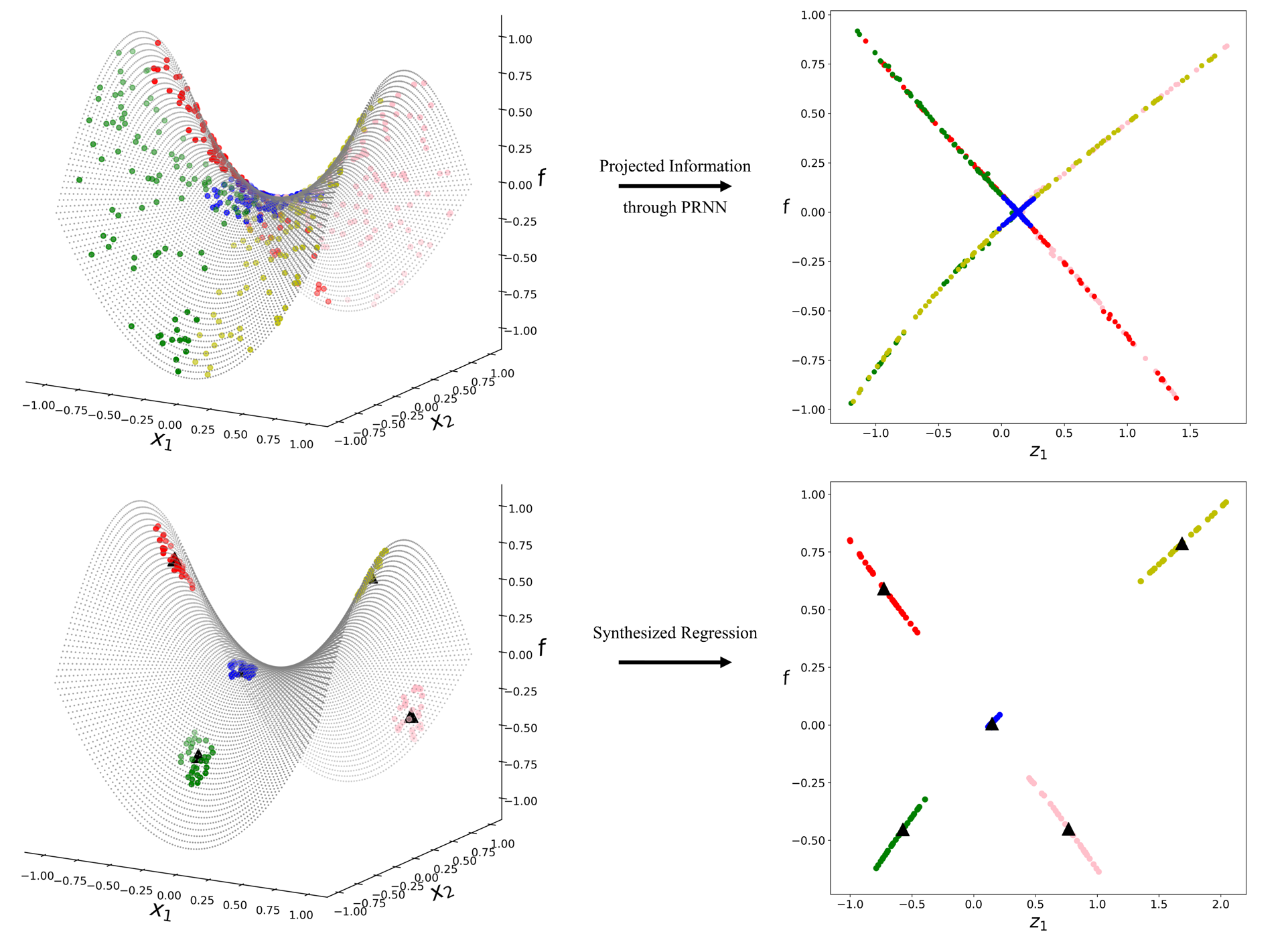
Level Set Learning with Pseudo-Reversible Neural Networks for Nonlinear Dimension Reduction in Function Approximation
Yuankai Teng, Zhu Wang, Lili Ju, Anthony Gruber, Guannan Zhang

SIAM Journal on Scientific Computing (SISC) [SIAM] [code]

Due to the curse of dimensionality and the limitation on training data, approximating high-dimensional functions is a very challenging task even for powerful deep neural networks. Inspired by the Nonlinear Level set Learning (NLL) method that uses the reversible residual network (RevNet), in this paper we propose a new method of Dimension Reduction via Learning Level Sets (DRiLLS) for function approximation. Our method contains two major components: one is the pseudo-reversible neural network (PRNN) module that effectively transforms high-dimensional input variables to low-dimensional active variables, and the other is the synthesized regression module for approximating function values based on the transformed data in the low-dimensional space. The PRNN not only relaxes the invertibility constraint of the nonlinear transformation present in the NLL method due to the use of RevNet, but also adaptively weights the influence of each sample and controls the sensitivity of the function to the learned active variables. The synthesized regression uses Euclidean distance in the input space to select neighboring samples, whose projections on the space of active variables are used to perform local least-squares polynomial fitting. This helps to resolve numerical oscillation issues present in traditional local and global regressions. Extensive experimental results demonstrate that our DRiLLS method outperforms both the NLL and Active Subspace methods, especially when the target function possesses critical points in the interior of its input domain.

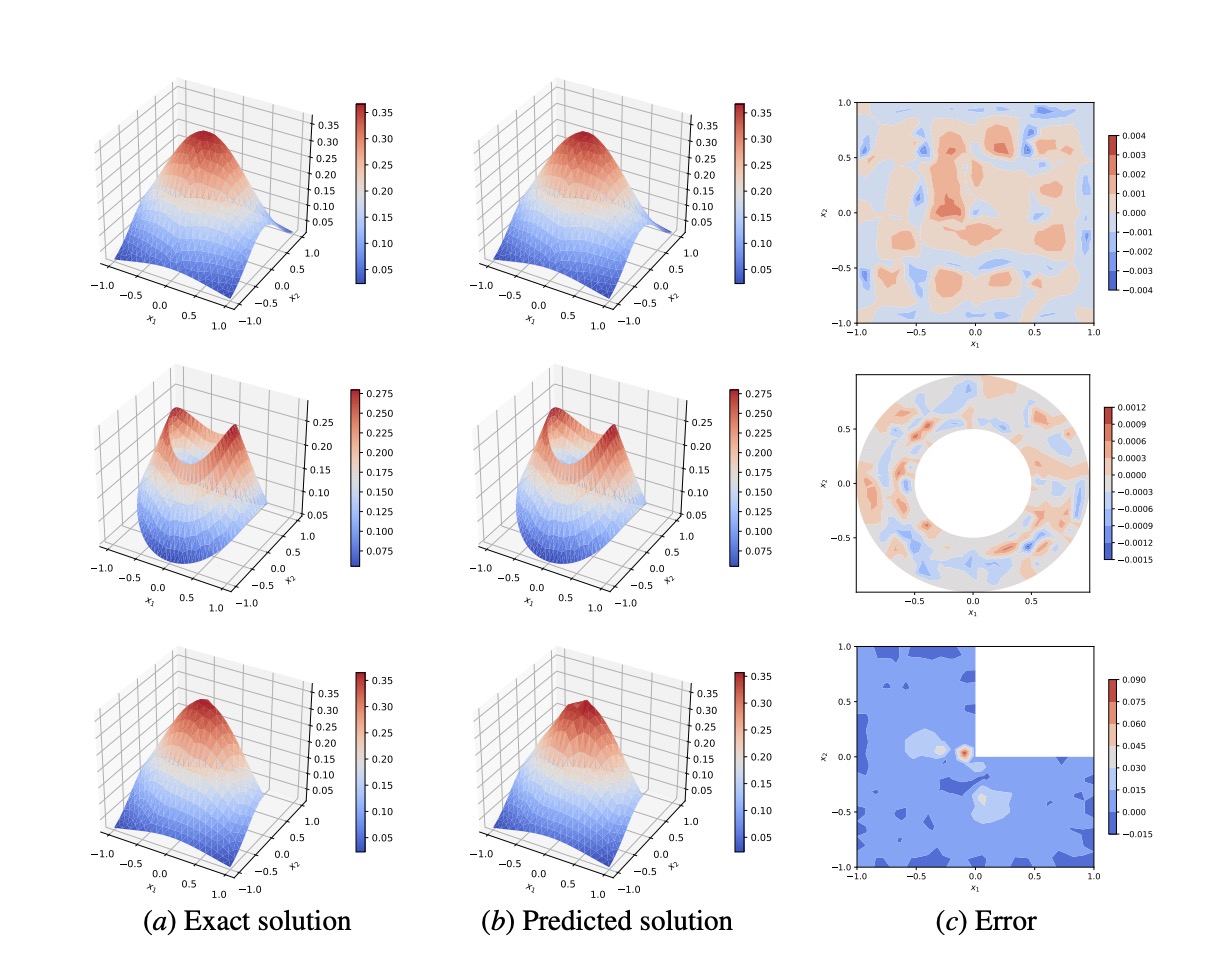
Learning Green's Functions of Linear Reaction-Diffusion Equations with Application to Fast Numerical Solver
Yuankai Teng, Xiaoping Zhang, Zhu Wang, Lili Ju

Proceedings of Third Mathematical and Scientific Machine Learning Conference (MSML'2022). [MSML22] [code]

Partial differential equations are commonly used to model various physical phenomena, such as heat diffusion, wave propagation, fluid dynamics, elasticity, electrodynamics and so on. Due to their tremendous applications in scientific and engineering research, many numerical methods have been developed in past decades for efficient and accurate solutions of these equations on modern computing systems. Inspired by the rapidly growing impact of deep learning techniques, we propose in this paper a novel neural network method, “GF-Net”, for learning the Green’s functions of the classic linear reaction-diffusion equation with Dirichlet boundary condition in the unsupervised fashion. The proposed method overcomes the numerical challenges for finding the Green’s functions of the equations on general domains by utilizing the physics-informed neural network and the domain decomposition approach. As a consequence, it also leads to a fast numerical solver for the target equation subject to arbitrarily given sources and boundary values without network retraining. We numerically demonstrate the effectiveness of the proposed method by extensive experiments with various domains and operator coefficients.

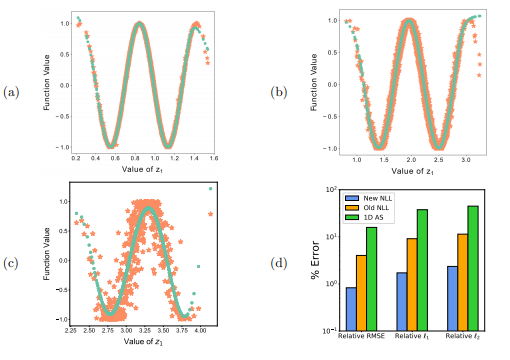
Nonlinear Level Set Learning for Function Approximation on Sparse Data with Applications to Parametric Differential Equations
Anthony Gruber, Max Gunzburger, Lili Ju,Yuankai Teng, Zhu Wang

Numer. Math. Theor. Meth. Appl. (2021). [DOI]

A dimension reduction method based on the "Nonlinear Level set Learning" (NLL) approach is presented for the pointwise prediction of functions which have been sparsely sampled. Leveraging geometric information provided by the Implicit Function Theorem, the proposed algorithm effectively reduces the input dimension to the theoretical lower bound with minor accuracy loss, providing a one-dimensional representation of the function which can be used for regression and sensitivity analysis. Experiments and applications are presented which compare this modified NLL with the original NLL and the Active Subspaces (AS) method. While accommodating sparse input data, the proposed algorithm is shown to train quickly and provide a much more accurate and informative reduction than either AS or the original NLL on two example functions with high-dimensional domains, as well as two state-dependent quantities depending on the solutions to parametric differential equations.

Interactive Binary Image Segmentation with Edge Preservation
Jianfeng Zhang, Liezhuo Zhang,Yuankai Teng, Xiaoping Zhang, Song Wang, Lili Ju [arXiv]

Binary image segmentation plays an important role in computer vision and has been widely used in many applications such as image and video editing, object extraction, and photo composition. In this paper, we propose a novel interactive binary image segmentation method based on the Markov Random Field (MRF) framework and the fast bilateral solver (FBS) technique. Specifically, we employ the geodesic distance component to build the unary term. To ensure both computation efficiency and effective responsiveness for interactive segmentation, superpixels are used in computing geodesic distances instead of pixels. Furthermore, we take a bilateral affinity approach for the pairwise term in order to preserve edge information and denoise. Through the alternating direction strategy, the MRF energy minimization problem is divided into two subproblems, which then can be easily solved by steepest gradient descent (SGD) and FBS respectively. Experimental results on the VGG interactive image segmentation dataset show that the proposed algorithm outperforms several state-of-the-art ones, and in particular, it can achieve satisfactory edge-smooth segmentation results even when the foreground and background color appearances are quite indistinctive.

Projects

Link to my [github public projects]

Low Frequency Objects In Unchanged Background Elimination Algorithm [Code]

I use RANSAC(Random Sample Consensus) method to eliminate the useless objects which randomly show in a series time-continuous unchanged background images. In this project I take the noise images as INPUT and give the modified clear background images as OUTPUT. The modified pictures will decline the noises which occurs in objects' 3D reconstruction by AI3D. The code is available in my github.

And this work is done during my internship in Farsee2 Technology.